Index

Links

[4. Applications.]

Linear differential equations.

A second order linear differential equation with constant coefficients is an equation of the type:



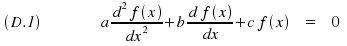
where a , b and c are real numbers.

Finding functions f(x) solutions of this kind of equations is simple. Consider the second order equation a·k² + b·k + c = 0, called the characteristic equation, and let k₁ and k₂ be its solution. There are three different cases:

1. k₁ and k₂ are different real numbers. Two particular solutions of equation (D.1) are f₁(x) = e ^x k₁ and f₂(x) = e ^x k₂ .
2. k₁ and k₂ are equal real numbers. Two particular solutions of equation (D.1) are are f₁(x) = e ^x k₁ and f₂(x) = x·e ^x k₁ .
3. k₁ and k₂ are different complex numbers: k₁ = p + iq , k₂ = p - iq. Two particular solutions of equation (D.1) are f₁(x) = e ^p x cos(qx) and f₂(x) = e ^p x sin(qx) .

The general solution of equation (D.1) is a linear combination of two particular solutions:  f(x) = A·f₁(x) + B·f₂(x) , where A and B are real numbers.

Back