Index

Links

[3. Schrödinger equations.]

Quantum operators.

An operator is a rule that transcripts (that is transforms) a given function in another function. Quantum mechanics makes use of operator for translating classical mechanical equations in quantum mechanical equations.

Let u be a classical mechanical quantity. Every classical mechanical quantity is defined by position and momentum, so u is a function of q and p : u = u (q₁ , q₂ , q₃ , p₁ , p₂ , p₃)

In quantum mechanics, an operator u_op corresponding to u is defined by means of the following two rules acting on the equation u = u (q₁ , q₂ , q₃ , p₁ , p₂ , p₃).

1. Substitute every occurrences of q_k with the operator "multiplication by q_k" and every occurrences of f (q_k) with the operator "multiplication by f (q_k)".
2. Substitute every occurrences of p_kⁿ with the operator  .

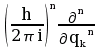For example, let u be the mechanical energy E given by (3.3). The operator E_op associated to E is:

.

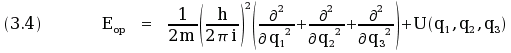Note that in (3.4) the expression U(q₁ , q₂ , q₃) means "multiply by U(q₁ , q₂ , q₃) ".

State description in classical mechanics

First Schrödinger equation