
First Schrödinger equation
 Quantum operators Quantum operators
|
Simplifying first Schrödinger equation 
|
[3. Schrödinger equations.]
First Schrödinger equation.
Let u be a given classical mechanical quantity; let uop
the quantum operator associated to u; the first Schrödinger equation
for u is
 .
.
For example, if u = E then the first Schrödinger equation for
the energy E is
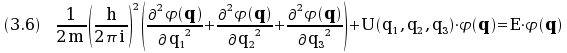 .
.
In the first Schrödinger equation the complex function φ (q) is the unknown
and u is a parameter. For every value of u there is a complex function
φ (q) that is a solution of the equation. However, not every φ (q) is
acceptable from a physical point of view, so some restrictions are imposed on φ (q).
One of such restrictions is the requirement that the quadratic integral of φ (q)
exists and is finite, that is φ (q) is acceptable as a solution only if the integral
∫ |φ (q)|² dx, extended over the domain to which x belongs,
is finite. Another requirement is that φ (q) must be finite for all values
of its argument q.
With such requirements, not for every value of u has the equation an acceptable
solution φ (q). The physical meaning of first Schrödinger equation is precisely
that only for certain values of u the equation has a solution φ (q): those
values are the admissible values for the physical quantity u.
Consider the equation (3.6) (first Schrödinger equation for energy E):
it admits solutions, compatible with the requirements on φ (q), only for a discrete
set of values of E, not for every value of E. Equation (3.6) thus determines the
admissible value for mechanical energy: they are the values giving a solution to the equation.
While in classical physics every value for the energy E is admissible, in quantum
mechanics only those values of the energy that satisfies the first Schrödinger equation
are admissible: this is the root of the quantization of the energy levels.
A brief recapitulation. Let u be a physical quantity; every value of u
is acceptable in classical physics. In quantum mechanics an operator uop
is defined according to certain rules, so to construct the equation
uopφ (q) = u·φ (q).
Some conditions of regularity are imposed on φ (q). The equation has solutions
only for certain values of u: those are the only acceptable values of u.
The physical quantity u has been quantized.
The values ui for which the first Schrödinger equation
uopφ (q) = u·φ (q)
has admissible solutions are called eigenvalues and the corresponding solutions
φi (q) are called eigenfunctions.
This words derives from the German terms eigenvert and eigenfunktion,
utilized by Schrödinger in his four articles entitled
Quantisierung als Eigenwertproblem (1926).
 Quantum operators Quantum operators
|
Simplifying first Schrödinger equation 
|