Bohr energy levels
 Simplifying first Schrödinger equation
|
State description in quantum mechanics 
|
[3. Schrödinger equations.]
Bohr energy levels.
In Bohr theory of the hydrogen atom, the angular momentum of the electron in its orbit is a
multiple of the quantity h/2π, so the energy of the electron is quantized.
The values En of the energy of the electron, called the energy levels,
are given by the formula
.
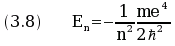This formula is derivable from the first Schrödinger equation. Consider an application
of the equation (3.7) to the hydrogen atom: The expression for the potential U is
U = - e²/r where e is the electron charge
and r is the distance from the electron.
In polar coordinates the equation (3.7) became
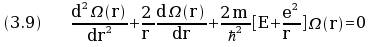
where Ω(r) is a function of the distance r.
The eigenvalues of the equation (3.9) are the values of E given by equation (3.8).
Thus the first Schrödinger equation gives a correct deduction of the energy levels of Bohr theory.
Values of E different from series (3.8) generate solutions Ω(r)
not acceptable. The figure shows the diagram of four solutions, two acceptable and
two not acceptable.
|
Simplifying first Schrödinger equation
|
State description in quantum mechanics
|