Mean values
 The effect of measurement on Ψ-function
|
Applications of the indeterminacy principle 
|
[5. Heisenberg indeterminacy principle.]
Mean values.
The mean value (also known as the expectation or the expected value) E(u) of a physical quantity u
can be calculated from the function Ψ using the following formula, where uop is the quantum
operator associated to u:
In equation (5.3) the operator uop acts on function Ψ .
We can also calculate the mean value of u² using the formula
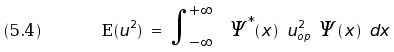
The indetermination
of u is given by the equation
.
A theorem, due to Paul Ehrenfest, states that the mean values of position and momentum of a particle with
mass m satisfy the equations of classical mechanics:
Equation (5.5) gives a connection between quantum mechanics and classical mechanics. If the indetermination
of position and momentum of a particle is so small that it can be ignored, then the particle acts according
to the classical laws of motion.
The amount of the indetermination is given by Heisenberg indeterminacy principle, which affirms that the
indetermination
and 
of two non commutative
entities satisfy the relation
If the non commutative entities are position and momentum, the equation (5.6) becomes
Note: 1 erg is the energy of a particle having a mass of 1 gm and a velocity of 1 cm/sec.
Equations (5.7) and (5.5) explain the success of classical mechanics in the realm of macroscopic objects.
|
The effect of measurement on Ψ-function
|
Applications of the indeterminacy principle
|